Ilmeteonelmondo

Le condizioni iniziali dei modelli meteo derivano dalla misurazione in tempo reale delle grandezze fisiche necessarie, come temperatura, umidità, vento, ecc. Queste misurazioni avvengono sia con stazioni meteo a terra che con i satelliti, ma ovviamente sono tutte soggette ad errori di misura. Ciò significa che dietro un insieme di valori misurati, in realtà esiste un'infinità di condizioni reali, tutte leggermente diverse fra loro, tutte equamente probabili all'interno degli errori di misura. I modelli ensembles tengono conto di questo fatto, per valutare quanto questi errori possano influenzare la previsione.

Dal punto di vista della modellizzazione del fenomeno fisico, i modelli ensembles (o probabilistici) usano sempre quella di un modello deterministico, ma le condizioni iniziali sono diverse. Il modello ensembles viene "eseguito" varie volte (di solito almeno 20), inizializzandolo ogni volta con dei valori opportunamente variati all'interno degli errori di misura delle condizioni attuali. Avendo ogni "run" un punto di partenza impercettibilmente diverso, le evoluzioni calcolate saranno per un certo lasso di tempo molto vicine tra loro, per poi allontanarsi sempre più a distanze di simulazione maggiori.

A causa del fatto che il modello va calcolato varie volte, solitamente la risoluzione dei modelli ensembles è minore dei loro rispettivi modelli deterministici, per limitare la complessità dei calcoli, quindi la singola evoluzione è di fatto meno precisa e non viene mai considerata come soluzione valida.

I risultati dei modelli ensembles vanno, invece, interpretati come distribuzioni di probabilità e come tali vanno considerati: ne va quindi calcolata la media, la varianza o la probabilità che si verifichi una condizione precisa.

La media degli ensembles fornisce solitamente la posizione più probabile delle grandi strutture atmosferiche (saccature, promontori, grandi depressioni) ma, soprattutto a distanze temporali alte, non equivale a nessuna soluzione possibile, perché il processo di media elimina tutte le strutture su scala medio-piccola, fondamentali per determinare la previsione meteo.

Lo spread o varianza (prima immagine a destra) è una misura di quanto e dove le varie soluzioni differiscono tra loro ed è fondamentale per valutare l'attendibilità della previsione. Solitamente lo spread aumenta con l'allungarsi della finestra temporale di previsione, ma mai allo stesso modo ovunque: in alcune aree può rimanere più basso, segnalando che in quell'area la previsione è meno affetta da errore e quindi più attendibile.

Le carte di probabilità (seconda immagine), infine, mostrano la percentuale di soluzioni che superano una certa soglia per una grandezza: per esempio si possono fare carte della probabilità di avere pressione minore di 1000 hPa, o temperatura inferiore a 0 gradi, ecc. o con una combinazione di grandezze si può ottenere la probabilità di neve.

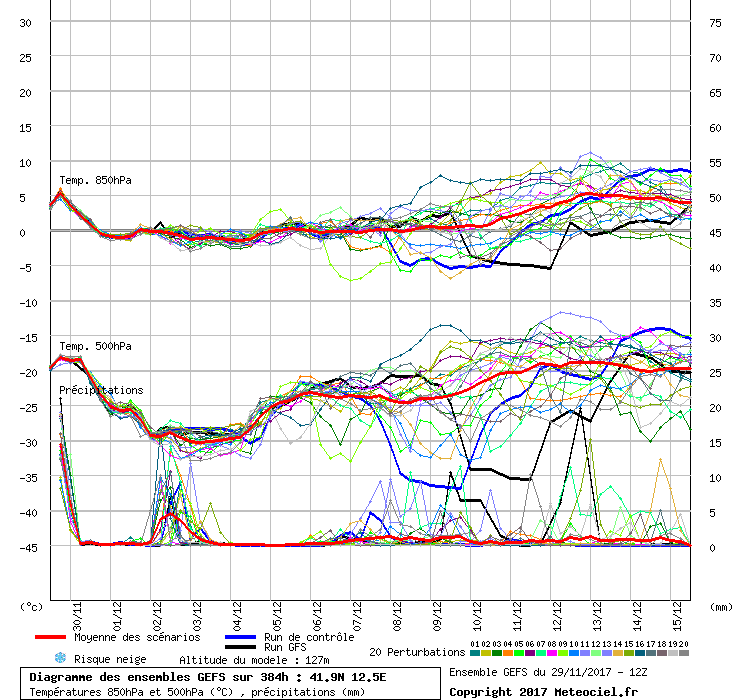
Un modo di visualizzare le informazioni date da un modello ensembles per una singola località è il cosiddetto grafico "a spaghi" o "a spaghetti" (terza immagine). Questi grafici mostrano l'evoluzione di tutte le soluzioni, ognuna rappresentata da uno spago. L'effetto è molto visivo, si può facilmente valutare la media e la distribuzione degli ensembles di varie grandezze, tipicamente le temperature a 500 hPa e a 850 hPa, valutando a colpo d'occhio la previsione più probabile e quanto sia attendibile.